Амплитуда гармонических колебаний

Колебания – это изменения состояний системы, повторяющиеся с определенной периодичностью. Если такие изменения можно описать по синусоидальному закону, то колебания называются гармоническими.

Классификация колебаний

Колебания могут быть:

механические;
электромеханические;
электромагнитные.

В зависимости от источника энергии система может совершать свободные либо вынужденные колебания. Свободные колебания происходят под действием собственных сил системы – внутренних. Такие колебания всегда имеют затухание, поскольку запас энергии расходуется на сопротивление трению и противодействию внешней среде.

Вынужденные колебания происходят в результате внешнего источника, поэтому могут быть незатухающими, если запас энергии периодически восполняется. Примером вынужденных колебаний в быту являются качели.

Характеристики гармонических колебаний

Для описания колебательного процесса есть несколько параметров, отражающих характер движения.

1. Амплитуда

Это максимальная величина отклонения положения системы от исходной позиции (равновесия). Единица измерения амплитуды А – метр. В литературе также можно встретить обозначение амплитуды «Х_max».

Для шарика, висящего на нитке (см. рисунок), положения 1 и 2 есть амплитуда его колебаний.

2. Период

Периодом называется минимальный промежуток времени, за который система возвращается в исходное состояние. Эта величина характеризует продолжительность одного законченного колебания и измеряется в секундах.

С математической точки зрения период Т равен отношению всего времени t, затраченного на изменение состояния, к количеству совершенных колебаний N:

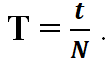
3. Частота

Это количество колебательных движений, произведенных за единицу времени. Частота измеряется в Герцах и является величиной, обратной периоду:

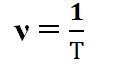
Если время колебаний составляет 2π секунд, то говорят о циклической или круговой частоте ω₀, которая связана с частотой ν и периодом Т следующим образом:

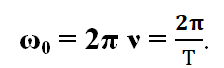
Круговая частота имеет размерность рад/с.

4. Фаза

Фаза колебаний φ характеризует временные границы, за которые рассматривается изменение системы. Начальной фазы (φ₀) – это позиция колеблющихся величин при t = 0.

Параметр φ – аргумент функции, описывающей колебательные движения.

Фаза находится по формуле:

φ = ω₀t + φ₀

Помимо перечисленных основных параметров есть еще понятия скорости и ускорения колебательного процесса, а также силы, которая вызывает гармонические колебания.

Уравнение

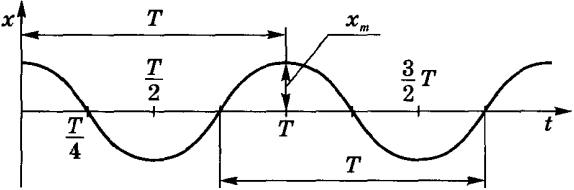
Гармонические колебания описываются следующими функциями:

x = Acos (ω₀t + φ),

x = Asin (ω₀t + φ)

Амплитуда зависит от начальных условий, в частности от энергии, вызывающей движение. Необходимо учитывать, что косинус и синус область допустимых значений от - 1 до 1.

Характеристики колебаний в задачах можно находить и графическим способом, используя кривую (синусоиду).

Примеры задач

Амплитуда колебаний некоторой точки на струне 2 мм, частота 1 кГц. Какой путь совершит эта точка за 0,4 с и каково будет перемещение точки?

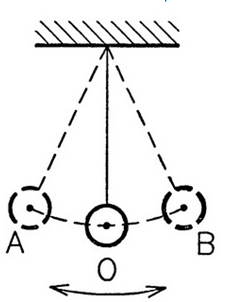
Решение. Точку струны можно представить в виде подвешенного шарика. Пусть начало колебаний находится в т. А. Тогда за период колебаний будет совершен путь из т. А в т. Б и обратно. Амплитуда колебаний равна расстоянию АО = ОВ. Т.е. растояние АВ есть двойная амплитуда. За полное колебание шарик совершит путь равный 4-м амплитудам: это путь шарика за период колебаний.

L₁ = 4·0,002 = 0,008 м.

Путь, совершенный точкой за все колебания, равен произведению пути за период на число колебаний N. При этом N = 1/Т = tν. Подставим известные значения частоты и времени: 0,4·1000 = 400 (колебаний).

Тогда точка на струне за все время колебаний совершит путь: 0,008·400 = 3,2 м.

Перемещение точки будет равняться 0, т.к. исходная позиция точки совпадает с конечной.

Пользуясь данными графика (изменения координаты колеблющегося объекта во времени), найти амплитуду, период и частоту колебаний, составить уравнение для колебаний и определить положение тела через 0,1 и 0,2 с от начала колебательного процесса.

Решение. На оси ОХ значение амплитуды составляет максимальное удаление от 0. Т.е. А = 30 см = 0,3 м.

Согласно рисунку, период – это отрезок между точками А и В. Время в т. А = 0, тогда как в т. В 1,6 с. Т.е. период Т = 1,6 – 0 = 1,6 с.

Частота ν = 1/Т = 1/1,6 = 0,625 Гц.

Поскольку в нулевой момент времени А ≠ 0, то колебания совершаются по закону косинуса. Поэтому уравнение будет иметь вид:

х = Аcos (2πν t) или х = 0,3cos 1,25πt.

Через 0,1 и 0,2 с координаты будут такими:

Х_0,1 = 0,3·cos (1,25·3,14·0,1) ≈ 0,29 м.

Х_0,2 = 0,3·cos (1,25·3,14·0,2) ≈ 0,30 м.