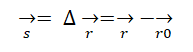Основные понятия
В кинематической теории тело принимается за материальную точку: движущийся объект обладает массой, но его геометрическими размерами можно пренебречь. Такое представление предмета облегчает решение многих задач, связанных с перемещением.
Наглядным примером служит поступательное движение.
Движение одного объекта всегда связано с окружающими предметами. Для описания движения выбирается тело отсчёта, относительно которого движется рассматриваемый объект.
Координатное поле, время как величина и тело отсчета в совокупности составляют систему отсчета. В ней отслеживается позиция материальной точки в отдельно взятый момент времени. Положение описывается законом движения в виде векторного уравнения либо зависимости координаты от времени, например, x = x (t), если это абсцисса.
Перемещение материальной точки – это отрезок между начальным и конечным пунктами движения. Данная величина векторная и представляется в следующем виде:
Перемещаясь, тело описывает кривую – траекторию.
Движение тела вдоль траектории от начальной точки до конечной составляет путь. Это величина выражена в метрах. Найти путь тела можно, умножив его скорость на время движения:
l = ʋ·t.
Таким образом, путь и перемещение не равны между собой. Путь не указывает направление, поэтому является скалярной величиной.
Если же речь идет о малом временном промежутке Δt, то длина пути Δl будет стремиться к значению перемещения и будет равна вектору . В случае движения по криволинейной траектории пройденный путь всегда превышает модуль вектора перемещения.
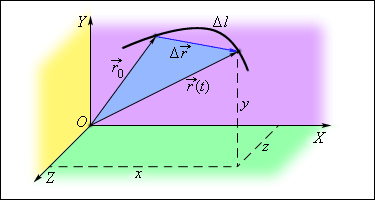
На рисунке ниже представлена система координат, траектория, векторы перемещения материальной точки.
Скорость также является вектором. Эта величина указывает, куда и насколько быстро происходит.
В кинематике используется понятие средней скорости:
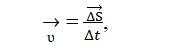
где величина Δt бесконечно мала, т.е. стремится к нулю.
Выделяют также понятие мгновенной скорости. Это скорость объекта в любой бесконечно малый промежуток времени. Ее вектор направлен по касательной к дуге траектории.
Изменение вектора скорости за любой стремящийся к нулю промежуток времени определяет векторная величина ускорение (мгновенное ускорение).
.png)
Если материальное тело двигается по окружности, вводятся понятия угловых скорости и ускорения, соответственно.
С математической точки зрения, ускорение есть производная скорости по времени.
Как задать движение
В кинематике существует три варианта задать движение:
- естественный;
- координатный;
- векторный.
Естественный способ также называется траекторным. Его применяют, когда траектория движения в системе отсчета задана по условию. В этом случае закон движения будет выражен уравнением зависимости расстояния (пути) от времени. Функция расстояния от времени s = f (t) может быть задана графически.
Закон движения при координатном задании описывается тремя временными зависимостями каждого из направлений (по оси x, по оси y, по оси z). В полученной системе уравнений при исключении времени можно определить траекторию тела.
При векторном способе составляется уравнение в векторном виде. Траектория будет представлена радиус-вектором из начальной точки до конечной в виде зависимости
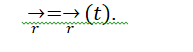
Для задания векторной величины необходимо знать направление и указать значение по модулю. При решении уравнений с векторами эти величины можно складывать, вычитать, делать проекции на оси координат.
Число уравнений, описывающих движение, зависит от числа степеней свободы объекта. Наиболее простыми случаями движения являются поступательное и вращательное (по окружности): с одной степенью свободы. В жизни таким образом движется, например, аттракцион колесо обозрения.
Пример более сложного движения – вращение тела с тремя степенями свободы (юлы, гироскопа).