Теория релятивистской механики
Ньютоновские законы не подходят для скоростей, соизмеримых со скоростью света, т.е. когда ʋ → с. В этих условиях действует специальная теория относительности (СТО). Помимо космических объектов СТО применима в физике ядра, квантовых процессах, при описании электромагнитных явлений, фотоэффекта и т.д.
СТО была изложена А. Эйнштейном в труде «К электродинамике движущихся тел». Ученый выдвинул основополагающие догмы, которые гласят, что в инерциальных системах отсчета:
- законы природы одинаковы;
- скорость распространения света в вакуумной среде одинакова (с = const).
Правило для сложения скоростей
В кинематике выведена теорема о сложении скоростей, которая гласит: при сложном движении вектор абсолютной скорости материальной точки есть сумма векторов относительной скорости и переносной:
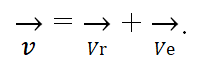
Физический смысл закона заключается в том, что скорость тела, которое движется относительно неподвижной системы отсчета, складывается из скорости относительно подвижной системы и скорости точки нахождения этого тела в подвижной системе отсчета.
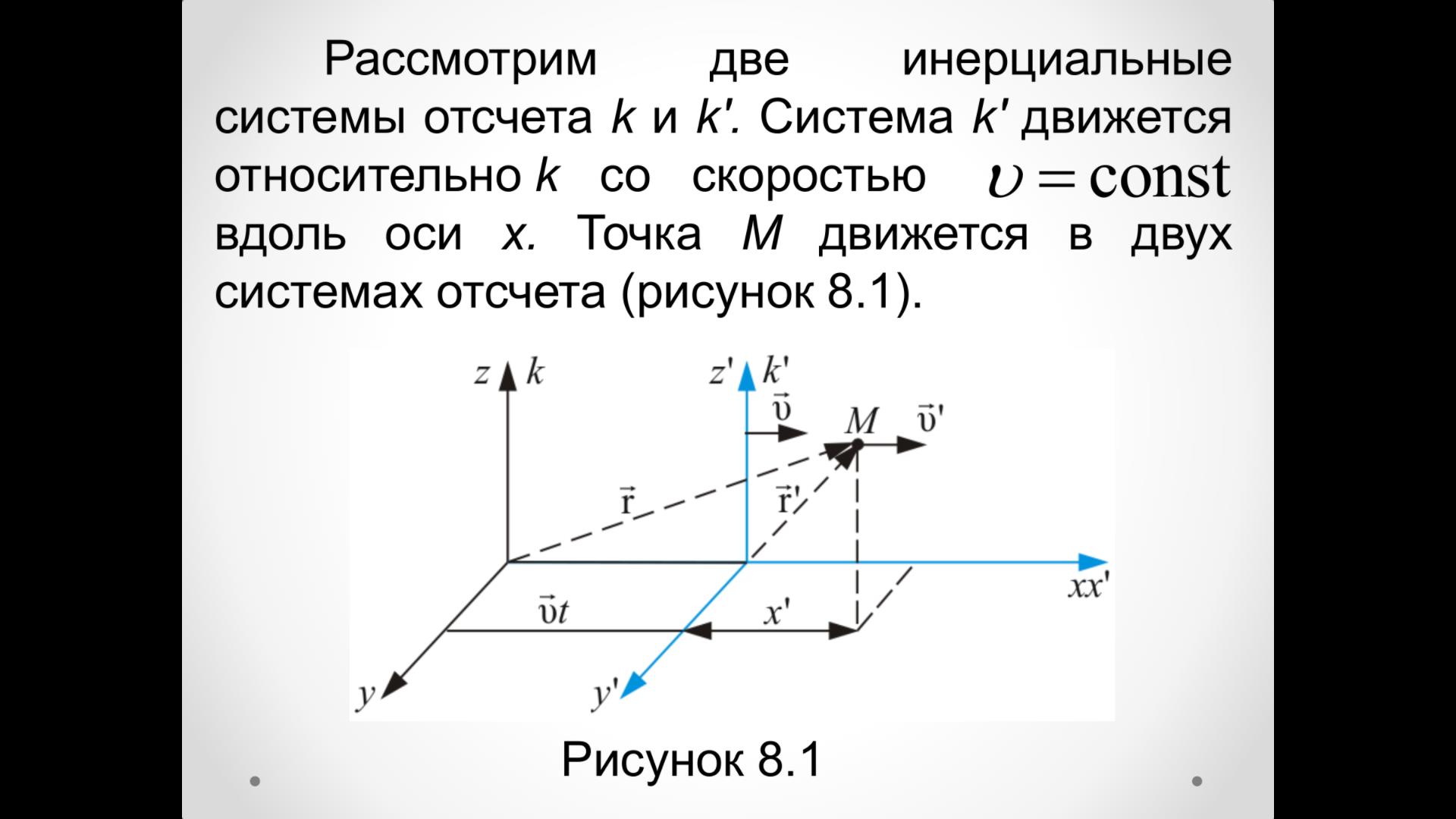
На рисунке приведены две системы отсчета k и k’. Т. М – объект, совершающий перемещение в обеих системах отсчета. Рассмотрим момент времени, когда t совпадает с t′
Для координаты точки М будут такими: t = t’, x = x + ʋt, y = y’, z = z’.
Эти равенства представляют собой преобразования Галилея, и они отвечают классической механике, когда во всех системах движение материальной точки происходит одинаково.
Представив выражение в векторном виде, получим:
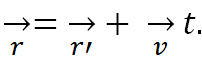
После дифференцирования по времени, получим как раз закон сложения скоростей. Графически он выглядит так:
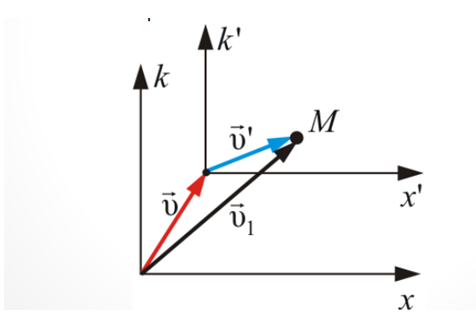
Преобразования Лоренца
Скорость света с = 2,998·108 м/с. Обозначим отношение v/c за параметр β. В случае скоростей, сравнимых с величиной скорости света, выражения Галилея имею вид:
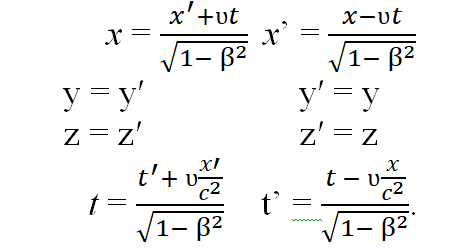
Данные уравнения показывают связь между координатами и временем в двух системах отсчета: неподвижной k и подвижной k′.
При малых значениях скоростей (ʋ<<c) (классическая механика) формулы соответствуют преобразованиям Галилея.
Формула для скорости
Представим выражения Лоренца для бесконечно малых величин и заменим β на v/c . Тогда:
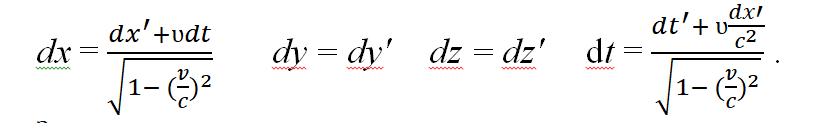
Зная, что скорость есть производная перемещения по времени, для каждой из координат в системе отсчета, имеем:
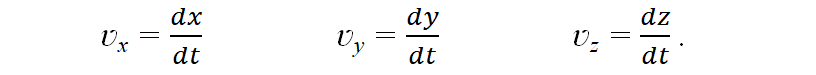
Аналогично и для подвижной системы отсчета:
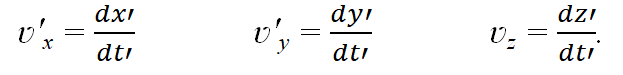
Тогда для абсциссы ʋx исходная формула после деления на dt будет иметь вид:
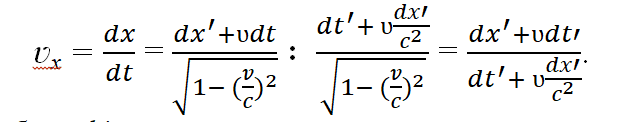
Сокращаем дробь на dt′:
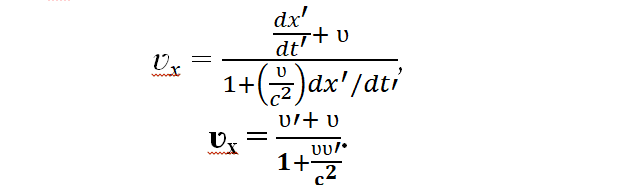
Мы пришли к уравнению для сложения скоростей в релятивистской механике.
Подставим скорость света в выражение для частного случая, когда ʋ→с.
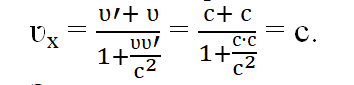
Это означает, что движение со скоростью, превышающей 3·108 м/с, запрещается данным правилом.
Преобразований Лоренца показывают, что свет распространяется с одинаковой скоростью для любого наблюдателя и не имеет значения находится наблюдатель в движении или в покое.
Пример задачи
- Самолет летит со скоростью относительно воздуха 300 км/ч в северном направлении. Северо-западный ветер подул со скоростью 100 км/ч. Чтобы продолжать курс на север, летчик должен удерживать машину под некоторым углом в сторону запада. Найти этот угол, а также скорость самолета относительно земли.
Решение.
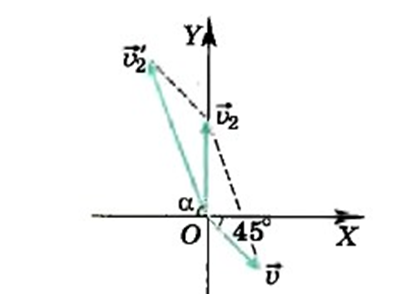
Северо-западный ветер имеет угол наклона 45°. Это отражено на рисунке.
Пусть система относительно земли будет неподвижной, а относительно воздуха – подвижной. По правилу сложения скоростей, скорость относительно земли 
будет равна сумме:
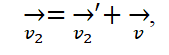
где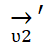 
- скорость, с которой самолет летит относительно воздушной системы;
- скорость ветра, который дует относительно земли.
По рисунку, проекции векторов скорости ветра и скорости самолета относительно ветра на ось абсцисс направлены противоположно, но равны по модулю. Тогда:
v′2cosα = v cosπ/4, откуда находим искомый угол α = arccos ((v/ v′2)cos π/4) = arccos ((100/300)0,707) ≈ 77 °.
В проекциях на ось ординат выражение имеет вид: v2y = v′2ysinα – vysinπ/4.
По правилам тригонометрии: sin α = . Найдем скорость v2y.
v2y = v′2y – vysinπ/4 ≈ 222 км/ч.