Этот принцип используется при работе с инструментами, например, со стамеской, плугом и прочими, а также для организации подъемных механизмов (трапов, пандусов).
Силы при движении по плоскости под углом
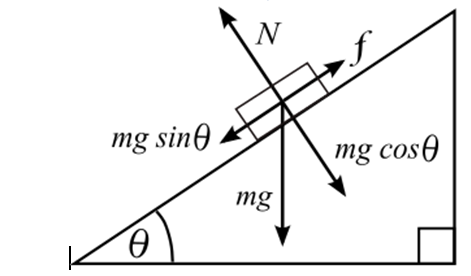
Рассмотрим, какие силы действуют на брусок, который скользит вниз на плоскости под углом наклона θ.
Согласно Второму закону Ньютона:
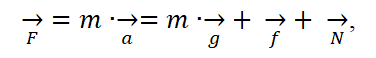
,
где ->N - сила реакции опоры;
->f – сила трения;
->a – вектор ускорения;
->g – вектор ускорения свободного падения;
m – масса бруска.
На рисунке вектор силы трения направлен вверх, поскольку по условию брусок съезжает по наклонной плоскости. Такое же направление будет и в случае состояния покоя. Если брусок двигается вверх, сила трения действует вниз.
Действия с векторами и величинами
При решении задач на движение по наклонной плоскости обязательно нужно привести рисунок и составить проекции векторов. Ось абсцисс рекомендуется направить вдоль направления движения, а ординат – перпендикулярно вверх, соответственно.
Сила трения f равна произведению реакции опоры на коэффициент трения . При проекции на оси получим N = mgcos θ, т.е.
f = mgcos θ.
Силу тяжести также следует представить через проекцию, выразив через угол θ:
m = mgsin θ.
Тогда исходное выражение для сил преобразуется так:
F = ma =mgsin θ + mgcos θ.
Отсюда, сокращая массу тела, получаем выражение для ускорения в общем виде:
a = g (sin θ ± cos θ).
Знак «−» необходим в случае спуска.
К частным случаям можно отнести:
нахождение в покое;
движение в отсутствии трения.
Тогда для первого случая можно записать следующее равенство:
mgsin θ = mgcos θ,
что означает равенство внешнего воздействия и сил тяжести (они уравновешивают друг друга).
При скольжении тела по поверхности сила трения может стремиться к нулю. Тогда имеет место выражение:
a = gsin θ.
При решении задач можно использовать для угла следующее правило. Если угол наклона плоскости составляет меньше или равен 0,1 радиан, то принимают его косинус за единицу, а синус будет равен числовому значению этого угла в радианах. Это же значение совпадает с тангенсом.
Выигрыш в силе
При движении под наклоном сила тяжести преодолевается легче, поэтому имеет место экономия приложенного усилия. Если расстояние, на которое перемещается груз, принять за величину l, а перпендикуляр к горизонтали (высота) – за h, то их соотношение и будет показывать, во сколько раз меньшую силу применили для данного движущегося объекта:
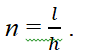
Экономия силы n – безразмерная величина.
Однако есть нюанс: за счет выигрыша в силе происходит удлинение пути, т.к. чем больше расстояние l, тем выше экономия.
Где применяется теории движения под наклоном
Примером из повседневной жизни является «наклонная плоскость» лестница. Действительно, легче дается подъем по более пологой и длинной лестнице, чем по короткой, но крутой.
Завинчивание самореза в какой-либо материал также происходит по принципу наклонной плоскости. При более мелкой резьбе внутри материала образующая плоскость имеет меньший угол наклона, при этом вкручивание винта происходит легче.
Типовые задачи
- Масса троллейбуса составляет 11 тонн. Он едет с горы равноускоренно. Угол наклона составляет 2,87°. Тяга равно 5 кН. Какова сила сопротивления?
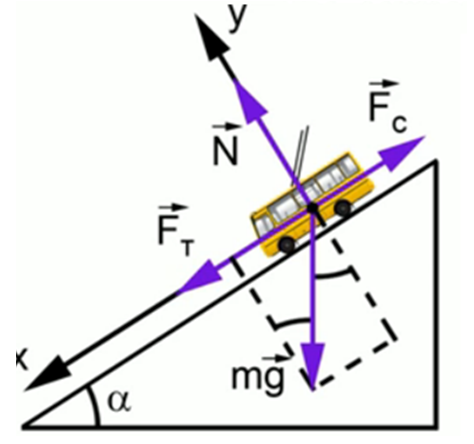
Решение. Запишем уравнения для всех сил:
m = m + + . Для проекций на ось Х:
mgsinα + Fт – Fс = 0.
Зная, что 2,87° ≈ 0,05 рад, то sinα = 0,05.
Подставляя известные величины, получаем искомую силу Fс = m∙g∙α + Fт =
= 11000∙9,8∙0,05 + 5000 ≈ 10,4 кН.
- Тело движется на плоскости под уклоном, длина этой плоскости составляет 15 м, а высота 3 м. Каков будет выигрыш в силе при спуске груза?
Решение. Экономия силы представляется как отношение длины плоскости к ее высоте. Тогда: n = l/h = 15/3 = 5 раз.
- На брусок некоторой массы m, спускающийся по наклонной под углом 30° плоскости. Сила, приводящая тело в движение, равна mg/2. Найти ускорение бруска при коэффициенте трения μ 0,065.
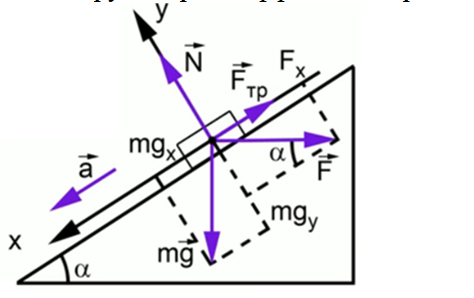
Решение.
Используя рисунок, распишем проекции всех сил на ось абсцисс в направлении движения бруска:
- сила тяжести m= mgsinα.
- действующая сила= Fcosα;
- трения = − μN = −μmgcosα.
Или: mgsinα – μN – Fcosα.
Т.к. величина реакции опоры не известна, используем проекции на ось ординат:
- сила тяжести – mgcosα
- реакция опоры N;
- сила –Fsinα.
Выразив значение N из полученной системы уравнений проекций, получим:
ma = mgsinα – μ(mgcosα + (mgsinα)/2) – mgcosα/2.
Откуда ускорение:
a = g(sinα – μcosα – (μsinα)/2 – 0,5cosα) = 9,8 (0,5-0,065∙0,866 – 0,065/4 – 0,866/2) ≈ ≈−0,054.
Вывод. Ускорение ˂ 0, значит, действующей силы недостаточно для спуска бруска.



