Первый, Второй и третий законы Ньютона

Исаак Ньютон – английский ученый, заложивший еще в XVII веке основы классической механики – три закона, приведенные в «Математических началах натуральной философии». Труд увидел свет в 1687 году.

В этой статье речь пойдет только о трех законах Ньютона.

I закон Ньютона

Первый постулат состоит в следующем. Если на тело не действуют никакие внешние силы, то оно либо находится в покое, либо движется равномерно и прямолинейно. Это означает, что для начала движения или изменения скорости необходимо применение к объекту внешнего воздействия.

В современной физической теории это утверждение называют законом инерции. Под термином инерция понимают способность материальной точки двигаться с постоянной скоростью и в неизменном направлении, если нет действия сторонних сил. В то же время, это свойство сопротивления внешнему влиянию на скорость. Таким образом, для изменения скорости объекта требуется применения силы извне.

Инертность у каждого физического тела разная. Количественно она определяется массой. Отсюда система отсчета, в которой работает Первый закон Ньютона, сегодня называется инерциальной. В жизни это подтверждается тем, что воздушный шарик легко сдвинуть с места, а тяжелый большой камень гораздо сложнее. Чем меньше масса, тем меньшую силу необходимо применить для придания телу ускорения.

В качестве источника внешнего воздействия законом рассматривается стороннее тело. Любое действие со стороны является противовесом внутренних сил материальной точки. Т.е. покоящийся предмет может находиться под скомпенсированным воздействием сил. Тогда Первый постулат есть закон сохранения движущегося состояния.

Представим все действующие силы в виде одной результирующей ƩF.

Если ƩF = 0, то ускорение будет тоже равно 0. При нулевом ускорении тело либо стоит на месте, либо не двигается без ускорения, т.е. скорость неизменна.

Задачи на I закон

Закон инерции не имеет графического выражения, поэтому решение задач на данную тему сводится к логическим рассуждениям и нахождению компенсирующей (результирующей) силы.

Классическим примером является задача про лифт, движущийся в шахте на тросе.

II закон Ньютона

Этот постулат показывает связь силы, массы объекта и ускорения его движения. Ускорение находится в прямой пропорциональной зависимости от действующей силы и в обратной – с его массой.

Формулировка: Действующая на тело сила есть произведение его массы на ускорение.

Математически зависимость выглядит так:

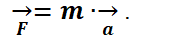
где

m – масса объекта, кг;

a – вектор ускорения м/с².

Формула F = m∙a составляет основу раздела «динамика».

Направление вектора ускорения совпадает с направлением вектора силы.

В реальных условиях на тело одновременно действуют различные силы. Для решения задач прежде всего необходимо найти суммарную силу.

Движение лыжника с горы – характерный пример комплексного воздействия.

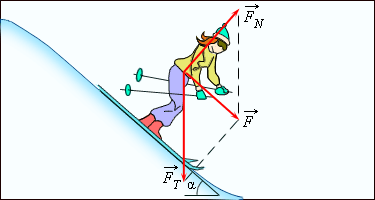
Как показано на рисунке, результирующая сила складывается из силы тяжести ->Ft , давления ->Fn и силы ->F , которая дает ускорение:

Отсюда видно, что в отсутствии ускорения ->F=0, что означает покой либо равномерное движение. Первый закон есть частный случай Второго.

Динамика оперирует также понятием импульса. Импульс является количественной мерой движения и находится как произведение вектора скорости на массу:

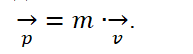
Тогда для инерциальной системы отсчета результирующая сила равна производной импульса тела по времени t:

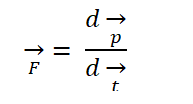
Примеры задач

В большинстве задач понятия ускорения и сил представляются в виде проекций векторов a_x, F_x. В примерах по умолчанию будем подразумевать именно проекции.

Простейшие задачи на применение второго закона сводятся к подстановке значений величин в формулу.

Найдите ускорение тела массой 600 г под действием внешней силы, равной 0,3Н.

Решение.

Зная, что a_x = , подставим значения массы в килограммах и силы в ньютонах.

Получаем: a_x = = 0,5 м/с².

Сила тяги двигателя машины составляет 1200 Н. Масса автомобиля 700 кг. За какое время автомобиль разгонится из состояния покоя до 72 км/ч?

Решение.

Для использования формулы Второго закона необходимо представить ускорение в виде отношения скорости ко времени. Машина была в покое, т.е. имела начальную скорость v₀, равную 0 м/с; конечная скорость v₁72 км/ч или 20 м/с.

Тогда:

F = m∙a = m∙(v₁ – v₀)/t, откуда время разгона t = m∙( v₁ – v₀)/F.

Подставив числовые значения, получим: t = 700∙(20 – 0)/1200 ≈ 11,7 с.

Т.е. для разгона автомобиля массой 700 кг до 72 км/ч при тяге двигателя 1,2 кН необходимо 11,7 секунды.

Исаак Ньютон в труде «Математические начала натуральной философии» дал формулировки трех законов, положивших основу классической теории механики. Первый закон детерминирует понятие движения. Во втором постулате обозначена взаимосвязь силы, массы и ускорения. Третий закон Ньютона касается взаимодействия двух тел между собой.

Формулировка

Если тело №1 воздействует с некоторой силой на тело №2, то тело №2 воздействует на тело №1 с силой, равной по модулю и противоположной по направлению.

При взаимодействии материальных точек силы всегда имеют общее происхождение и должны компенсировать друг друга, но этого не происходит, поскольку объекты их приложения разные.

Математическая запись постулата такова:

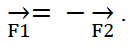
Принимая во внимание Второй закон Ньютона, получим выражение:

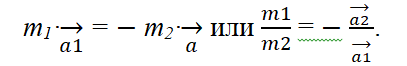
Т.е. массы взаимодействующих объектов обратно пропорциональны их ускорениям.

В физике Третий закон Ньютона называют также законом действия и противодействия.

Современные ученые трактуют закон следующим образом. Две материальные точки взаимодействуют между собой с силами, которые равны по модулю, направлены противоположно и действуют по прямой, проходящей через эти точки.

Третий закон в реальных условиях

По дороге едет автомобиль. Дорожное покрытие подталкивает колёса вперед, сами колеса при этом толкают дорогу назад. Это приводит в движение всю машину.
При взлете вертолет толкает воздух вниз, тогда как воздушная масса толкает вертолет наверх, заставляя подниматься.
В бассейне пловец под водой ускоряется от борта, совершая ногами толчок назад, но движение пловца направлено вперед.

Пример задачи на Третий закон

Кабина лифта имеет ускорение a = 3 м/с². На полу лежит груз, имеющий массу 15 кг. Найти силу, с которой груз действует на пол при движении лифта вверх.

Решение.

Милы, действующие на груз:

реакция опоры ->N;
сила тяжести ->Ft

По условию вектор ускорения направлен вертикально. Тогда:

m∙a = F_т∙+ N;

m∙a = m∙g + N;

N = m∙ (a +g) = 15∙(3+9,8) = 192 Н.

Согласно III закону, сила реакции опоры по модулю равна силе, действующей на пол со стороны груза, а значит, равна также 192 Н.