Краткая суть теории
Макроскопическое тело состоит из молекул, которые, в свою очередь, сформированы атомами. В атоме находятся ядра и электроны, а внутри ядра находятся нейтроны и протоны. Частицы нейтроны содержат еще более мелкие частицы – кварки. На следующем уровне, согласно теории струн, кварки включают в себя тончайшие и длинные нити наподобие струн. Т.е. струны – это шестой уровень строения вещества.
Типы струн:
- открытые;
- закрытые.
Если струна открытого типа, она способна присоединяться к другой струне, образуя новую. Закрытые струны участвуют в описании гравитации и лежат в основе развития квантовой гравитации. В пространстве закрытые струны образуют петли, т. е. представляют собой замкнутый контур.
Теория струн утверждает принцип суперсимметрии: каждой частице бозону соответствует определенный фермион.
Число измерений
Самой привычной для нашей жизни является трехмерная модель описания явлений, включающая геометрические параметры: длина, ширина, высота. Четвертым измерением принято считать время. Т.е. большинство физических закономерностей оперирует понятиями пространство-время (модель 4D). В теории струн задействовано гораздо больше размерностей пространства-времени: подразумевается, что их не менее десяти.
Компактизация
Однако при описании физических явлений и процессов нет необходимости учитывать все разнообразие измерений. Перед физиками в теории струн стоит задача представления такого алгоритма, при котором дополнительные измерения не будут отслеживаться экспериментально.
Для этого используют компактизацию. Метод позволяет изменять количество измерений. По предположениям ученых, «лишние» измерения образуют замкнутый контур в виде кругов.
Согласно М-теории, размер компактизиованного измерения крайне мал: порядка
10-33 см. На сегодняшний день подтвердить это экспериментально не представляется возможным.
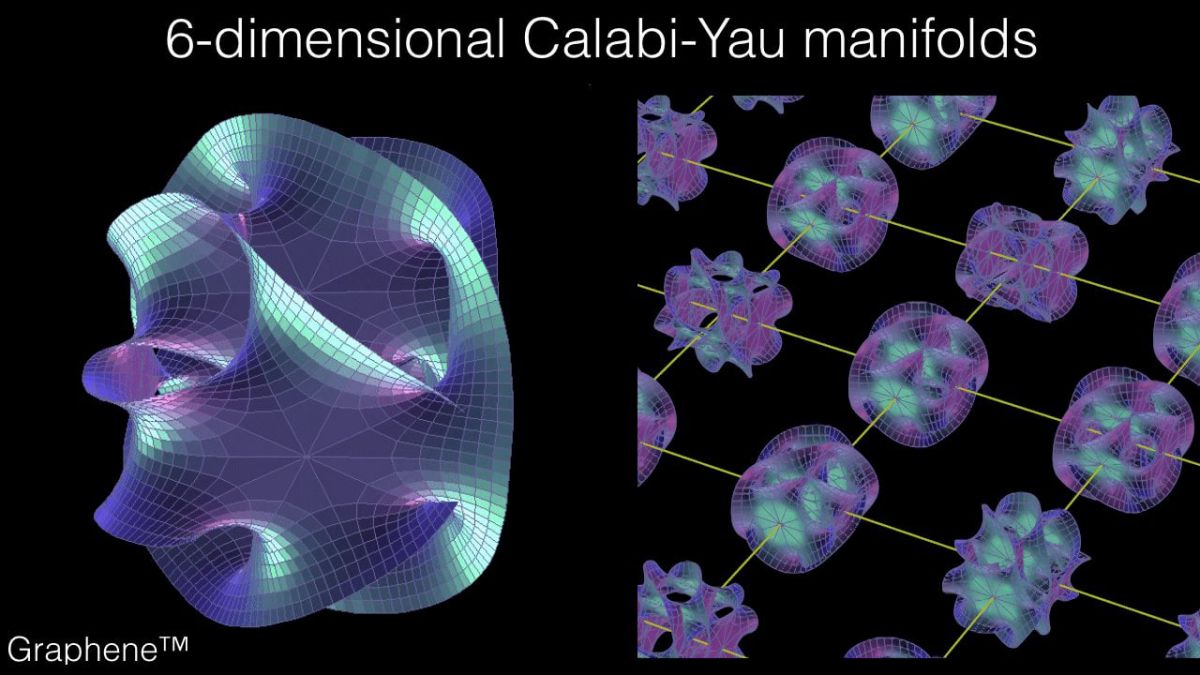
Многообразия Калаби-Яу
В струнной теории предполагается, что дополнительные к четырем известным измерениям 4D имеют форму шестимерного многообразия, названного в честь Калаби, выдвинувшего гипотезу о таком пространстве, и Яу, который смог ее доказать.
На рисунке приведена компьютерная модель пространства Калаби-Яу.
Без применения компактизации невозможно моделирование процессов. С помощью 6-мерных многообразий Калаби-Яу описывают многие явления на ядерном уровне.
Зеркальная симметрия
Использование пространства Калаби-Яу позволило объединить несколько струнных теорий. Суть теории заключается в том, что пространства Калаби-Яу могут не совпадать с точки зрения геометрии, но иметь одинаковую физическую составляющую на субатомном уровне при применении их как дополнительные измерения в струнной теории. Считается, что многообразия такого типа зеркально симметричные.
С помощью зеркальной симметрии (ЗС) современные физики проводят вычисления в теории струн. Её используют при описании квантовых полей и при описании физики элементарных частиц.
Составляющие теории:
- гомологическая ЗС;
- SYZ-гипотеза.
Т-дуальность
ЗС оперирует понятием Т-дуальностью. Преобразования в этой концепции распространяются на такие пространства, в которых хотя бы одна из областей топологически представляет собой окружность. Тогда ее радиус R меняется на величину 1/R, а струнные состояния становятся высокоимпульсными.
Иными словами, струна IIA, обернутая вокруг пространства дважды, отобразится как струна IIB, имеющая двойной импульс.
Краткое содержание гипотезы SYZ
В 1996 г. Э. Строминджер, Ш. Яу, Э. Заслоу выдвинули свою теорию понимания ЗС. Было предложено разбивать многообразие на упрощенные компоненты, составляя затем из них пространство, зеркально симметричное исходному.
Примером применения гипотезы является двумерный объект тор. Его можно рассматривать как объединение множества кругов. Аналогично, любая четырехмерная K3-поверхность раскладывается на две 2-мерные составляющие.
В общем случае SYZ-гипотеза дает возможность расширять Т-дуальность до любого количества измерений. В этом случае необходимо Т.е. гипотетический тор может быть n-мерным, тогда необходимо комплексное разложение многообразия Калаби-Яу с количеством размерностей n.
Таким образом, гипотеза Строминджрера-Яу-Заслоу сводится к тому, что зеркальная симметрия подобна применению Т-дуальности к n-мерным торам в конкретный момент времени. Это геометрический подход реализации ЗС.